(1)证明:∵AB=AD=BD,∴∠BAD=60°,∵AB=AD,BE=DE,∴AC⊥BD,∵四棱柱ABCD-A1B1C1D1是直四棱柱,∴DD1⊥平面ABCD.∵AC⊂平面ABCD,∴AC⊥DD1,∵AC⊥BD,AC⊥DD1,BD∩DD1=D,∴AC⊥平面BB1D1D;(2)解:取B1D1的中点F,连接EF,以E为坐标原点,分别以EA,EB,EF所在直线为x,y,z轴建立空间直角坐标系.∵,BE=1.∴B(0,1,0),B1(0,1,2),D1(0,-1,2),A(,0,0),O(,-,1),,.
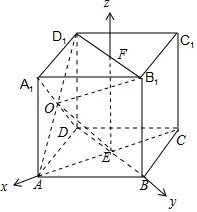
(1)证明:∵AB=AD=BD,∴∠BAD=60°,∵AB=AD,BE=DE,∴AC⊥BD,∵四棱柱ABCD-A1B1C1D1是直四棱柱,∴DD1⊥平面ABCD.∵AC⊂平面ABCD,∴AC⊥DD1,∵AC⊥BD,AC⊥DD1,BD∩DD1=D,∴AC⊥平面BB1D1D;(2)解:取B1D1的中点F,连接EF,以E为坐标原点,分别以EA,EB,EF所在直线为x,y,z轴建立空间直角坐标系.∵,BE=1.∴B(0,1,0),B1(0,1,2),D1(0,-1,2),A(,0,0),O(,-,1),,.

(1)证明:∵AB=AD=BD,∴∠BAD=60°,∵AB=AD,BE=DE,∴AC⊥BD,∵四棱柱ABCD-A1B1C1D1是直四棱柱,∴DD1⊥平面ABCD.∵AC⊂平面ABCD,∴AC⊥DD1,∵AC⊥BD,AC⊥DD1,BD∩DD1=D,∴AC⊥平面BB1D1D;(2)解:取B1D1的中点F,连接EF,以E为坐标原点,分别以EA,EB,EF所在直线为x,y,z轴建立空间直角坐标系.∵,BE=1.∴B(0,1,0),B1(0,1,2),D1(0,-1,2),A(,0,0),O(,-,1),,.

(1)证明:∵AB=AD=BD,∴∠BAD=60°,∵AB=AD,BE=DE,∴AC⊥BD,∵四棱柱ABCD-A1B1C1D1是直四棱柱,∴DD1⊥平面ABCD.∵AC⊂平面ABCD,∴AC⊥DD1,∵AC⊥BD,AC⊥DD1,BD∩DD1=D,∴AC⊥平面BB1D1D;(2)解:取B1D1的中点F,连接EF,以E为坐标原点,分别以EA,EB,EF所在直线为x,y,z轴建立空间直角坐标系.∵,BE=1.∴B(0,1,0),B1(0,1,2),D1(0,-1,2),A(,0,0),O(,-,1),,.

(1)证明:∵AB=AD=BD,∴∠BAD=60°,∵AB=AD,BE=DE,∴AC⊥BD,∵四棱柱ABCD-A1B1C1D1是直四棱柱,∴DD1⊥平面ABCD.∵AC⊂平面ABCD,∴AC⊥DD1,∵AC⊥BD,AC⊥DD1,BD∩DD1=D,∴AC⊥平面BB1D1D;(2)解:取B1D1的中点F,连接EF,以E为坐标原点,分别以EA,EB,EF所在直线为x,y,z轴建立空间直角坐标系.∵,BE=1.∴B(0,1,0),B1(0,1,2),D1(0,-1,2),A(,0,0),O(,-,1),,.

(1)证明:∵AB=AD=BD,∴∠BAD=60°,∵AB=AD,BE=DE,∴AC⊥BD,∵四棱柱ABCD-A1B1C1D1是直四棱柱,∴DD1⊥平面ABCD.∵AC⊂平面ABCD,∴AC⊥DD1,∵AC⊥BD,AC⊥DD1,BD∩DD1=D,∴AC⊥平面BB1D1D;(2)解:取B1D1的中点F,连接EF,以E为坐标原点,分别以EA,EB,EF所在直线为x,y,z轴建立空间直角坐标系.∵,BE=1.∴B(0,1,0),B1(0,1,2),D1(0,-1,2),A(,0,0),O(,-,1),,.

(1)证明:∵AB=AD=BD,∴∠BAD=60°,∵AB=AD,BE=DE,∴AC⊥BD,∵四棱柱ABCD-A1B1C1D1是直四棱柱,∴DD1⊥平面ABCD.∵AC⊂平面ABCD,∴AC⊥DD1,∵AC⊥BD,AC⊥DD1,BD∩DD1=D,∴AC⊥平面BB1D1D;(2)解:取B1D1的中点F,连接EF,以E为坐标原点,分别以EA,EB,EF所在直线为x,y,z轴建立空间直角坐标系.∵,BE=1.∴B(0,1,0),B1(0,1,2),D1(0,-1,2),A(,0,0),O(,-,1),,.

(1)证明:∵AB=AD=BD,∴∠BAD=60°,∵AB=AD,BE=DE,∴AC⊥BD,∵四棱柱ABCD-A1B1C1D1是直四棱柱,∴DD1⊥平面ABCD.∵AC⊂平面ABCD,∴AC⊥DD1,∵AC⊥BD,AC⊥DD1,BD∩DD1=D,∴AC⊥平面BB1D1D;(2)解:取B1D1的中点F,连接EF,以E为坐标原点,分别以EA,EB,EF所在直线为x,y,z轴建立空间直角坐标系.∵,BE=1.∴B(0,1,0),B1(0,1,2),D1(0,-1,2),A(,0,0),O(,-,1),,.
设平面OB1D1的一个法向量为.

设平面OB1D1的一个法向量为.
由,取x=2,得.

由,取x=2,得.

由,取x=2,得.

,∴|cos<>|==.

,∴|cos<>|==.

,∴|cos<>|==.

,∴|cos<>|==.
∴直线OB与平面OB1D1所成的角的正弦值为.

∴直线OB与平面OB1D1所成的角的正弦值为.



